Acknowledgements: This blogpost discusses joint work between the author and Matthias Cosler, Christopher Hahn, Daniel Mendoza, and Frederik Schmitt.
Introduction
A rigorous formalization of desired system requirements is indispensable when performing any verification task, such as model checking, synthesis, or runtime verification. This often limits the application of verification techniques, as writing formal specifications is an error-prone and time-consuming manual task, typically reserved for experts in the field. In our recent work, we have developed a framework and associated tool, called nl2spec, for leveraging Large Language Models (LLMs) to derive formal specifications (in LTL and similar temporal logics) from unstructured natural language.
Going forward, we are excited about the potential role of LLMs in the hardware verification domain. In this blogpost, we highlight our work on nl2spec and point out some observations which we find relevant for continued work in this space.
Overview of Prerequisites
Model Checking and Temporal Logic
Linear-time Temporal Logic (LTL) is a temporal logic that forms the basis of many practical specification languages, such as the IEEE property specification language (PSL), Signal Temporal Logic (STL), or System Verilog Assertions (SVA).
LTL formulae may be used to describe properties about the future states of an execution trace or execution path. LTL formulae are built over a base set of propositional variables, which act as the atoms of the logic, and are used to describe basic properties of states within an execution trace. The logic also contains the logical truth and falsity constants, as well as the standard connectives of propositional logic: conjunction (∧), disjunction (∨), negation (¬), and implication (→). These formulae are augmented with temporal modalities U (until) and X (next), which relativize a formula against an abstract notion of time, permitting formulae to make reference to events occurring later in an execution trace. There are several derived operators, such as Fφ ≡ trueUφ and Gφ ≡ ¬F¬φ. Fφ and Gφ state that φ holds in some and every future state of the trace, respectively.
Operators can be nested: GFφ, for example, states that φ has to occur infinitely often. LTL specifications describe a system’s behavior and its interaction with an environment over time. For example, given a process 0, a process 1, and a shared resource, the formula G(r0 → Fg0) ∧ G(r1 → Fg1) ∧ G¬(g0 ∧ g1) states that whenever a process requests (ri) access to a shared resource it will eventually be granted (gi). The subformula G¬(g0 ∧ g1) ensures that grants given are mutually exclusive. The formal syntax and semantics of LTL can be found in Appendix A of our nl2spec pre-print.
One can evaluate a system’s adherence LTL properties, over an unbounded space of execution traces, using property verifiers based on model checking. For example, in the space of formal hardware verification, SystemVerilog Assertions (SVAs), support specifying LTL properties over the execution traces that can be realized on a SystemVerilog RTL implementation. Cadence’s JasperGold property verifier leverages model checking algorithms to check an RTL specification’s adherence to user-defined SVAs.
Large Language Models
LLMs are large neural networks typically consisting of up to 176 billion parameters. They are pre-trained on massive amounts of data, such as “The Pile.” Examples of LLMs include the GPT and BERT model families and open-source models, such as T5 and Bloom. LLMs are Transformers, i.e., the state of the art neural architecture for language processing. Additionally, Transformers have shown remarkable performance when being applied to classical problems in verification, reasoning, and the auto-formalization of mathematics and formal specifications. See our nl2spec pre-print for detailed citations.
While fine-tuning neural models on a specific translation task remains a valid approach showing also initial success in generalizing to unstructured natural language when translating to LTL, a common technique to obtain high performance with limited amount of labeled data is so-called “few-shot prompting.” The language model is presented with a natural language description of the task accompanied with a few examples that demonstrate the input-output behavior. The nl2spec framework and our ongoing work rely on this technique.
Overview of nl2spec
Our core contribution towards deriving LTL specifications from natural language is a new methodology to first decompose natural language input into sub-translations using LLMs. The nl2spec framework then provides an interface to interactively add, edit, and delete these sub-translations instead of having to grapple with the entire formalization at once (a feature which is missing in similar work, like NL2LTL and Lang2LTL).
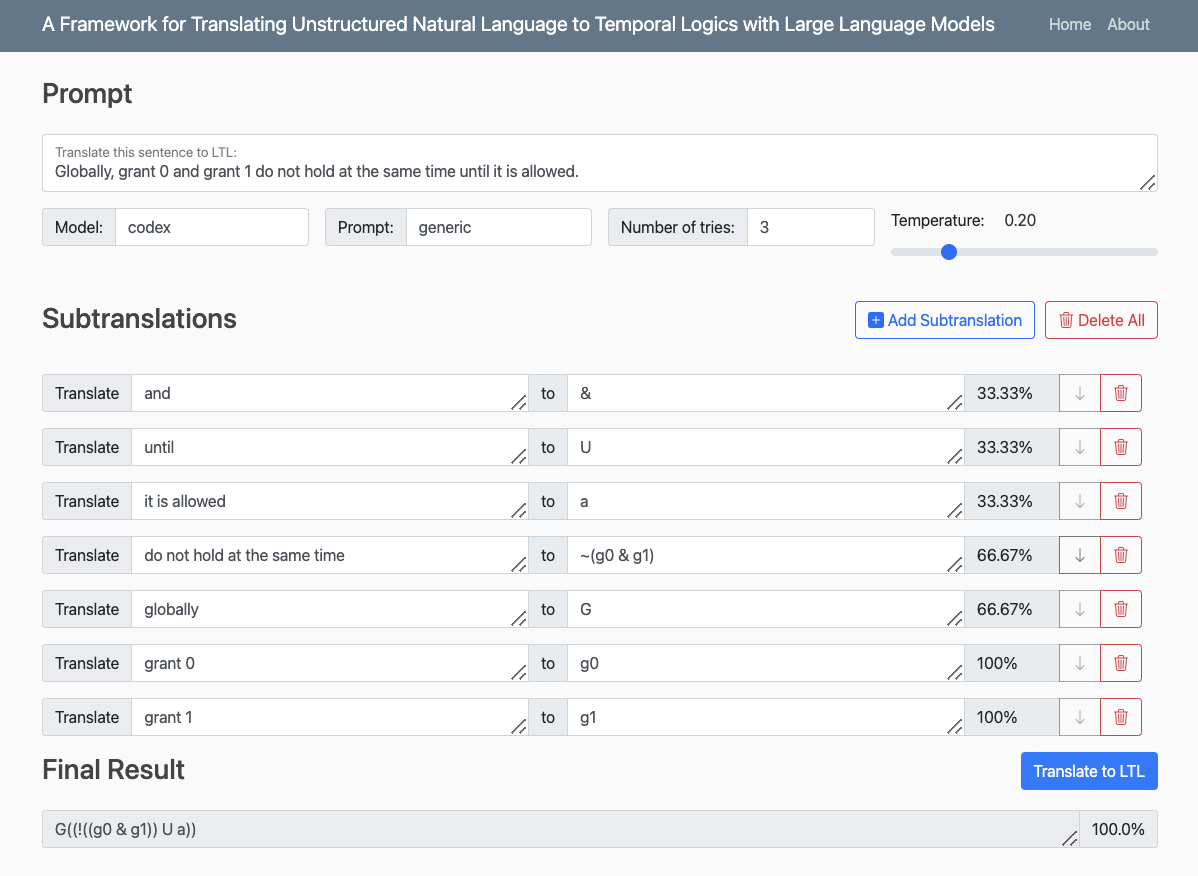
Figure 1. A screenshot of the web interface for nl2spec.
Figure 1 above shows the web-based frontend of nl2spec. As an example, we consider the following system requirement given in natural language: “Globally, grant 0 and grant 1 do not hold at the same time until it is allowed.” The tool automatically translates the natural language specification correctly into the LTL formula G((!((g0 & g1)) U a)). Additionally, the tool generates sub-translations, such as the pair (“do not hold at the same time”, !(g0 & g1)), which help in verifying the correctness of the translation.
Consider, however, the following ambiguous example: “a holds until b holds or always a holds”. Human supervision is needed to resolve the ambiguity on the operator precedence. This can be easily achieved with nl2spec by adding or editing a sub-translation using explicit parenthesis (see Section 4 of our preprint for more details and examples). To capture such (and other types of) ambiguity in a benchmark data set, we conducted an expert user study specifically asking for challenging translations of natural language sentences to LTL formulas.
The key insight in the design of nl2spec is that the process of translation can be decomposed into many sub-translations automatically via LLMs, and the decomposition into sub-translations allows users to easily resolve ambiguous natural language and erroneous translations through interactively modifying sub-translations. The central goal of nl2spec is to keep human supervision minimal and efficient. To this end, all translations are accompanied by a confidence score, alternative suggestions for sub-translations can be displayed and chosen via a drop-down menu, and misleading sub-translations can be deleted before the next loop of the translation. We evaluate the end-to-end translation accuracy of our proposed methodology on the benchmark data set obtained from our expert user study.
We direct the reader to our pre-print for more details of the overall approach and instructions on running our open-source nl2spec artifact.
Towards LLMs for Hardware Verification
Our work on nl2spec takes a small step towards leveraging the power of LLMs for democratizing computer systems verification in general, and hardware verification in particular. During this project, we have made a few observations that we believe will be relevant for future work in this space:
- Intermediate representations, such as our sub-translations, are effective in resolving natural language ambiguity and providing specification interpretability.
- LLMs may prove useful in specializing existing properties to target new designs. For example, certain functional correctness properties may persist across microarchitectural generations, but their precise formulation will change to reflect design differences.
- Few-shot prompting aligns well with how hardware designers communicate various desired or undesired system properties, e.g., memory consistency model specifications in the form of litmus tests, the CVE database, the CWE database, simulation traces, and so on.
- LLM-assisted hardware verification will likely require new methods of circuit abstraction and decomposition due to prompt length limitations. If a user formulates a natural language property with respect to a monolithic circuit which is too large for the LLM, both the property and design will require decomposition, a process which we believe can be assisted by LLMs as well.
- We started our exploration of LLM-assisted verification by devising a feedback loop between a human (the verification engineer) and an LLM-assisted specification generator. However, we also envision a valuable feedback loop between the specification generation and an LTL property verifier, like a model checker. We believe this scenario will be particularly useful in the space of automated hardware repair, where hardware design is to be modified to conform to some specification (e.g., iterative circuit repair against formal specifications).
In Conclusion
Overall, this blogpost highlights some early work (our own and that of others) in the space of LLM-assisted computer systems verification, with a focus on hardware verification. We have provided some intuition behind the nl2spec framework for translating unstructured natural language to temporal logics. A limitation of our approach is of course a reliance on computational resources at inference time. This is a general limitation when applying deep learning techniques. Both, commercial and open-source models which we have experimented in our work, however, provide easily accessible APIs to their models. Notably though, the quality of initial translations might be influenced by the amount of training data on logics, code, or math that the underlying neural models have seen during pre-training.
At the core of nl2spec lies a methodology to decompose the natural language input into sub-translations, which are mappings of formula fragments to relevant parts of the natural language input. Our pre-print introduces an interactive prompting scheme that queries LLMs for sub-translations and an interface for users to interactively add, edit, and delete the sub-translations, which eschews users from manually redrafting the entire formalization to fix erroneous translations. Our modest user study shows that nl2spec can be efficiently used to interactively formalize unstructured and ambiguous natural language.
About the Author: Caroline Trippel is an Assistant Professor of Computer Science and Electrical Engineering at Stanford University. Her research on architectural concurrency and security verification has been recognized with IEEE Top Picks distinctions, an NSF CAREER Award, the 2020 ACM SIGARCH/IEEE CS TCCA Outstanding Dissertation Award, and the 2020 CGS/ProQuest® Distinguished Dissertation Award in Mathematics, Physical Sciences, & Engineering.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


