General Matrix Multiplication (GEMM) is a fundamental operation in machine learning and scientific computing. It is the classic example of an algorithm that benefits greatly from GPU acceleration due to its high degree of data parallelism. More recently, efficient GEMM implementations on modern GPU accelerators have proven crucial to enabling contemporary advances in large language models (LLMs). Conversely, the explosive growth of LLMs has driven investment into GPUs’ raw hardware capabilities as well as architectural innovations, with GEMM as the yardstick by which GPU performance is measured. As such, understanding GEMM optimization can inform a deeper understanding of modern accelerators.
In this tutorial on GEMM optimization, we discuss some practical aspects of orchestrating a pipeline of data in order to efficiently feed the GPU’s tensor cores. In the context of GEMM kernel design, pipelining refers to the idea of overlapping copy and matrix-multiply-accumulate (MMA) operations through maintaining multiple data buffers. We focus on the NVIDIA Hopper architecture as it features highly robust and programmable asynchronous execution capabilities that we can leverage for effective pipelining. In general, there are two pipelining strategies that are effective on the Hopper architecture:
- Warp-specialization. Specializing warps into producers (data transfer) and consumers (compute), and having them run concurrently.
- Multistage. Masking data transfer by using asynchronous copy (TMA on Hopper or
cp.asyncon Ampere) to load the next set of data, while computing on the current set. Warps take on both producer and consumer roles.
Using tools from the CUTLASS library, we will explain how to write a GEMM kernel that uses a multistage design, paying careful attention to how to write the necessary synchronization logic using the CUTLASS Pipeline classes. A broader discussion, including that of warp-specialization and a performance evaluation, can be found in our original article on the Colfax Research website.
The big picture: “Feeding the beast”
There are 2 main actions in a GEMM kernel: copying the numbers to the correct memory addresses, and multiply-accumulating them. The former action is handled by copy instructions: TMA in Hopper, cp.async in Ampere, and vanilla copy in earlier architectures. The latter action, since the Volta architecture in 2017, has become the exclusive business of the tensor cores.
Through many generations, the tensor cores have become a beast at consuming the numbers fed to them. For instance, the H200 SXM GPU’s tensor cores can deliver up to 3,958 TFLOPS (TeraFLOPs per second). On the other hand, the memory bandwidth of the same H200 SXM5 GPU is only 4.8 TB/s (TeraBytes per second). This data transferring speed is much slower than the tensor cores’ speed, and oftentimes is not trivial to fully utilize! As such, a common theme of CUDA programming — and GEMM kernel design in particular — is to figure out how to copy numbers fast enough to keep the tensor cores busy. We call this process “feeding the beast.”
In general, there are two overarching strategies to “feed the beast,” which are complementary and function at different scopes (grid vs. block). The first strategy is effective threadblock scheduling, which entails distributing the computation among the CTAs to obtain good load balancing and a higher rate of L2 cache hits. We don’t discuss this here, but instead refer curious readers to the techniques of threadblock rasterization and persistent kernels. The second strategy is to overlap copying with math operations. In particular, while the tensor cores are busy multiplying a batch of numbers that they receive, we should tell the copying units to copy the next batch of numbers. That way, we effectively hide part of the copying latency. This is the goal of pipelining.
Pipelining Illustrated
Figure 1 illustrates a theoretical pipeline of LOAD and MMA. Here, LOAD refers to the process of copying operand matrix tiles from global memory (GMEM) to shared memory (SMEM), and MMA refers to the tensor core operation that multiplies the operand tiles stored in SMEM. As shown in the figure, by overlapping two LOADs with two MMAs, we save 2 units of time.
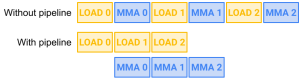
Figure 1. Pipelining 3 loads and 3 MMA steps.
One problem that arises from contemplating Figure 1 is: where do LOAD_1 and LOAD_2 copy the data into? Clearly, we don’t want subsequent loads to overwrite the data copied in by prior loads before MMA can compute on that data. Nor do we want unnecessary stalls caused by waiting on SMEM to become free to write into. Otherwise, the supposed gain of 2 units of time will not actually be achieved.
A simple solution to this problem is to reserve twice as much memory in SMEM than is needed by MMA and use them in an alternating fashion. This strategy is called double buffering and is illustrated in Figure 2. Of course, we can generalize to having more than two alternating buffers. Doing so creates more opportunity for overlap, allowing for more efficient use of the available hardware, at the cost of using more SMEM.
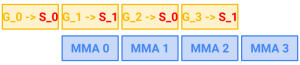
Figure 2. Pipelining with two alternating SMEM stages.
It is not trivial to implement pipelines correctly and efficiently. Programmers must handle the multiple buffers as well as asynchronous load calls across multiple threads. In the next section, we show how to implement pipelining via a CUTLASS abstraction: the Pipeline class.
The CUTLASS Pipeline abstraction
CUTLASS’ asynchronous Pipeline classes serve as an effective abstraction to manage copy and compute across multiple data buffers and participating threads. They include the classes PipelineAsync, PipelineTmaAsync, and PipelineTransactionAsync, for which “Pipeline” is a generic reference.
We first explain how a CUTLASS Pipeline orchestrates the pipelining of data at a high-level. Let buffers be a shared memory buffer with N stages. We wish to synchronize between a producer writing data to the buffers (e.g., TMA) and a consumer operating with that data as it becomes available (e.g., WGMMA).
Barriers. To synchronize the buffer stages across the producer and the consumer, a Pipeline adheres to the standard acquire and release model that uses locks to manage accesses to the buffers. To this end, let full_barrier and empty_barrier be two arrays of barrier objects, both of size N. These barrier objects possess a phase bit value which is initialized to 0 and flips between 0 and 1.
Concretely, these barrier objects will be mbarrier objects resident in SMEM. An mbarrier object is initialized both with the aforementioned phase bit as well as an arrival count. It then supports arrive-on and wait operations and flips its phase based on reaching the arrival count threshold. Importantly, the values of these barrier objects can and should be visible to all threads.
Thread-local pipeline state. Next, we have the PipelineState class as a thread-local enumerator that serves to track the thread’s current index and phase, with the number N of stages passed in as a template parameter. The index takes on integer values modulo N, and the phase is either 0 or 1. Moreover, the ++ operator for the PipelineState class is overloaded so that the index is incremented modulo N, and the phase is flipped when the index increments to 0.
Synchronization. We now explain how the barrier objects and thread-local pipeline states are used to synchronize producers and consumers. To avoid confusion, let us distinguish the producer action from the producer thread(s) issuing that action, as these may potentially be decoupled (think of TMA). First, the producer action will flip the phase of full_barrier[i] to signal that it has filled the ith stage of the buffer, so that the consumer threads can now read from it. Similarly, the consumer threads will flip the phase of empty_barrier[i] to signal that they have finished consuming the ith stage of the buffer, so that the producer can now write to it.
Note that we are agnostic as to exactly how the producer action or the consumer threads flip the phase bit in SMEM, as long as it is done via the arrival count mechanism. For example, all the consumer threads could collectively act to increment the arrival count, or one consumer thread per warp could be elected to do the same.
Finally, each thread, whether consumer or producer, keeps track of a phase to match against the phases of the barrier objects, and in fact threads taking on both consumer and producer roles will need to track both phases. These “internal” phases of the threads need to be flipped as well as the kernel proceeds through iterations of its mainloop.
Four pipeline methods. Now let pipeline be an instance of a Pipeline class initialized with pointers to full_barrier and empty_barrier, and let pipe_state be an instance of a PipelineState class. Then pipeline can invoke the following four key methods:
pipeline.producer_acquire(pipe_state). Blocks the calling thread until the phase ofempty_barrier[pipe_state.index()]flips againstpipe_state.phase().pipeline.producer_commit(pipe_state). Signalsfull_barrier[pipe_state.index()]to increment its arrival count.pipeline.consumer_wait(pipe_state). Blocks the calling thread until the phase onfull_barrier[pipe_state.index()]flips againstpipe_state.phase().pipeline.consumer_release(pipe_state). Signalsempty_barrier[pipe_state.index()]to increment its arrival count.
In the description of the blocking instructions producer_acquire and consumer_wait, by flipping against the phase of pipe_state we mean that, for example, if the current phase of the barrier is 0, then the method blocks if the phase of pipe_state is 0 and doesn’t block if it is 1.
Note that as written, the pair of methods (producer_acquire, consumer_release) and (producer_commit, consumer_wait) are completely symmetric in functionality. However, if the Pipeline class in question is PipelineTmaAsync, then full_barrier is wrapped as an instance of the cutlass::arch::ClusterTransactionBarrier class and the signaling mechanism for full_barrier is handled by the TMA load method itself via incrementing the transaction count. In this case, the producer_commit method is actually a no-op; we return to this point below. However, in pseudocode we will still insert producer_commit if the TMA copy is not written out, as we do now.
Putting it all together, the following pseudocode shows the four pipeline methods in action:
using PipelineState = typename cutlass::PipelineState;
// We initialize smem_pipe_write to start with an opposite phase
// (i.e., 1 instead of 0), since the buffers start out as empty.
PipelineState smem_pipe_write = cutlass::make_producer_start_state();
PipelineState smem_pipe_read;
for (int i = 0; i < total_steps; ++i) {
pipeline.producer_acquire(smem_pipe_write);
// Acquire data (e.g. TMA, cp.async, etc.)
pipeline.producer_commit(smem_pipe_write);
++smem_pipe_write;
pipeline.consumer_wait(smem_pipe_read);
// Compute workload (e.g. WGMMA)
pipeline.consumer_release(smem_pipe_read);
++smem_pipe_read;
}
We find the above code snippet helpful for illustrating the producer/consumer acquire and release pattern. We invite readers to go through a few steps of the loop while keeping track of all of the involved states, and to connect this pseudocode with the verbose description of synchronization given prior.
However, this snippet features a serialized execution flow in which producer and consumer operations never run concurrently, and hence it is not useful in practice. In an effective pipelined workload, the producer and the consumer must overlap. We next discuss the multistage kernel design that gives one way to accomplish this.
Multistage kernel design
Let’s use the TMA-specialized version of the Pipeline class, PipelineTmaAsync, to create a 2-stage pipeline used in a Hopper GEMM kernel that overlaps TMA with WGMMA, which is the primitive tensor core instruction on Hopper that involves 128 threads doing the MMA (i.e., 1 warpgroup of threads). We assume the reader is familiar with the syntax of TMA and WGMMA in CUTLASS, which we discussed in detail in two previous blogposts, or is otherwise willing to take this syntax on faith. As such, we omit the preparation and explanation of the tensors that go into the cute::copy and cute::gemm calls.
using MainloopPipeline = typename cutlass::PipelineTmaAsync;
using PipelineState = typename cutlass::PipelineState;
typename MainloopPipeline::Params params;
// number of bytes transferred by TMA load per stage (A and B)
params.transaction_bytes = TmaTransactionBytes;
params.role = MainloopPipeline::ThreadCategory::ProducerConsumer;
params.is_leader = threadIdx.x == 0;
params.num_consumers = 128;
// Disregard clusters for this example
auto cluster_shape = Shape{};
// pipeline_storage is instance of cutlass::PipelineTmaAsync::SharedStorage
// Has full_barrier and empty_barrier as members
// Located in the SharedStorage struct that manages objects in smem
MainloopPipeline pipeline(shared_storage.pipeline_storage, params, cluster_shape);
__syncthreads();
PipelineState smem_pipe_write =
cutlass::make_producer_start_state();
PipelineState smem_pipe_read;
// Prepare tensors for GEMM
// ...
// Issue the first TMA load with leader thread
if(threadIdx.x == 0) {
pipeline.producer_acquire(smem_pipe_write);
BarrierType *tmaBar = pipeline.producer_get_barrier(smem_pipe_write);
// smem_pipe_write.index() == 0
copy(tma_load_a.with(*tmaBar, 0), tAgA(_,0), tAsA(_,0));
copy(tma_load_b.with(*tmaBar, 0), tBgB(_,0), tBsB(_,0));
++smem_pipe_write;
}
for (int i = 0; i < k_tile_count - 1; ++i) {
// Only leader thread issues TMA load
if(threadIdx.x == 0) {
pipeline.producer_acquire(smem_pipe_write);
BarrierType *tmaBar = pipeline.producer_get_barrier(smem_pipe_write);
auto write_stage = smem_pipe_write.index();
copy(tma_load_a.with(*tmaBar, 0), tAgA(_,i+1), tAsA(_,write_stage));
copy(tma_load_b.with(*tmaBar, 0), tBgB(_,i+1), tBsB(_,write_stage));
++smem_pipe_write;
}
// Compute on the completed load from prior iteration
pipeline.consumer_wait(smem_pipe_read);
auto read_stage = smem_pipe_read.index();
// WGMMA
warpgroup_arrive();
gemm(tiled_mma, tCrA(_,_,_,read_stage), tCrB(_,_,_,read_stage), tCrC);
warpgroup_commit_batch();
warpgroup_wait();
pipeline.consumer_release(smem_pipe_read);
++smem_pipe_read;
}
// Handle the last compute iteration
pipeline.consumer_wait(smem_pipe_read);
auto read_stage = smem_pipe_read.index();
warpgroup_arrive();
gemm(tiled_mma, tCrA(_,_,_,read_stage), tCrB(_,_,_,read_stage), tCrC);
warpgroup_commit_batch();
warpgroup_wait();
pipeline.consumer_release(smem_pipe_read);
// Epilogue for writing out accumulator
axpby(alpha, tCrC, beta, tCgC);Here, in each iteration of the main loop, the (i+1)th TMA load is issued asynchronously and the ith WGMMA computation executes, noting that smem_pipe_write and smem_pipe_read are offset from each other by one.
In this pseudocode, note that the producer_acquire method of the PipelineTmaAsync class method does the following internally in order to set the transaction bytes count needed for TMA, where stage and phase are the index and phase of its PipelineState argument:
if (barrier_token != BarrierStatus::WaitDone) {
empty_barrier_ptr_[stage].wait(phase);
}
if (params_.is_leader) {
full_barrier_ptr_[stage].arrive_and_expect_tx(params_.transaction_bytes);
}Moreover, we use the producer_get_barrier method with argument smem_pipe_write in order to retrieve a pointer to full_barrier[smem_pipe_write.index()], as needed by the TMA TiledCopy objects tma_load_a and tma_load_b in the cute::copy call.
With the cute::copy call thus linked to the mbarrier object full_barrier of the pipeline, we can then use the transaction count-based completion mechanism of TMA to signal the consumer that the buffer is ready to be used, obviating the need to invoke producer_commit from the pipeline object itself. This is why CUTLASS makes producer_commit a no-op for PipelineTmaAsync.
This way of structuring the pipelining allows for overlapping data transfer and computation, delivering on the potential of asynchronous operations to hide latency. Finally, though we used TMA in this example, a similar technique is available in the Ampere architecture with cp.async.
Conclusion
In this article, we have presented a comprehensive picture of the pipelining technique. We introduced its goal of hiding latency by overlapping memory copy and math operations, and why this is integral to good performance. Then we presented the multistage pipelining design, which involves leveraging asynchronous copy operations such as TMA in Hopper or cp.async in Ampere to mask data transfer. We hope this tutorial can serve as a useful resource for readers looking to understand modern GEMM kernel design more deeply.
About the Author: Jay Shah is a research scientist in accelerated computing at Colfax International, a leading Silicon Valley-based provider of custom computing solutions. He leads Colfax’s efforts to optimize ML/AI applications for the latest NVIDIA GPU architectures. Prior to joining Colfax, he earned a Ph.D. in mathematics from the Massachusetts Institute of Technology in 2017 and held several academic positions, where he conducted and published research on topology and higher category theory.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


