Data management research has recently been paying more attention on how to run machine learning algorithms efficiently on massive datasets. This blog post focuses on three recent research papers that identify time-consuming data processing operations in machine learning workloads. The reported performance results suggest that some of these operations can be significantly accelerated in hardware. These ideas are part of a broader effort to design systems that better support machine learning in real-world deployments, which we will cover more extensively in a future blog post.
On-the-fly data transformations for machine learning
Training generalized linear models requires fast descent methods to find the minimum of a function. One obstacle towards combining this task with database processing is differences in the data layout. Specifically, SQL operations in a database are performed on a small batch of data at a time where each attribute is stored separately (i.e. a column-oriented format). However, gradient-based optimization methods assume complete access to the dataset and read all attributes of a data point on every iteration (i.e. a row-oriented format). A recent VLDB paper proposes an FPGA-based descent method that achieves high cache efficiency with a columnar data layout and shows impressive efficiency for real-world machine learning tasks. By using coordinate descent instead of gradient descent it suffices to access one feature at a time in a batched access pattern, while the empirical convergence rate of the two algorithms is similar. The overall performance of the training thus hinges on the efficiency of data transformation and processing, which can be accelerated with a dedicated FPGA-based stochastic coordinate descent engine.
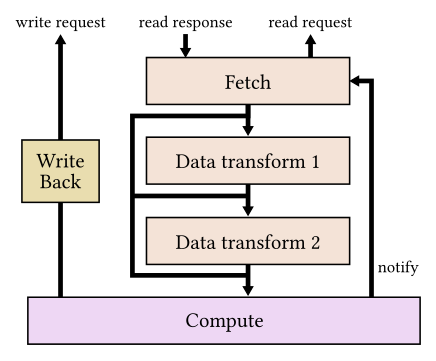
Diagram of FPGA-based stochastic coordinate descent engine. Adapted from Figure 11 of K. Kara, K. Eguro, C. Zhang, G. Alonso: “ColumnML: Column-Store Machine Learning with On-The-Fly Data Transformation.” PVLDB 12(4).
The FPGA-based coordinate descent engine consists of a Fetch unit, two Data Transformation units, a Compute unit and a Write Back unit. The Fetch unit requests a data partition for processing. The Compute unit calculates the gradient of the current partition and updates the local inner product. The Compute unit is designed to consume 16 single-precision floating points (one 64-byte cache line) per clock cycle, for a total throughput of 12.8 GB/sec at 200MHz. The Write Back unit performs model updates and writes the computed inner products back to memory. The two Data Transformation units support optional on-the-fly delta-encoding decompression and AES-256 decryption without any impact on the total throughput. The performance evaluation shows that by using multiple stochastic coordinate descent engines one can perform coordinate descent at a rate of 17 GB/sec (the FPGA memory bandwidth in the test system) for real-world machine learning tasks.
Tuple-oriented compression for machine learning
Compression is a very effective technique to fit large datasets in memory, especially if datasets are sparse. General lossless compression libraries like zlib or Snappy can be used when the data is at rest, but they require decompressing the payload before data processing and re-compressing the result at the end. The overhead of compression and decompression can be substantial if a data item is accessed multiple times. Prior research has developed query-friendly compression techniques that allow common SQL operations to be evaluated on compressed data. This improves the efficiency of throughput-bound data processing operations, as more bytes can be processed per second. However, the ability to evaluate SQL operations on compressed data is not sufficient for machine learning workloads that rely extensively on matrix operations, in particular matrix-vector and matrix-matrix multiplications. An upcoming SIGMOD paper proposes a new compression technique that operates at the granularity of individual tuples and can evaluate common matrix operations on compressed data without decoding the input.
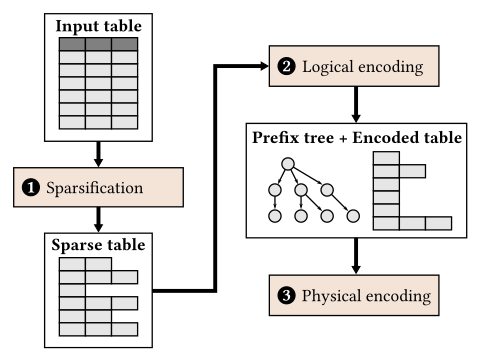
Tuple-oriented compression for machine learning workloads. Adapted from Figure 3 of F. Li, L. Chen, Y. Zeng, A. Kumar, X. Wu, J. Naughton, J. Patel: “Tuple-oriented Compression for Large-scale Mini-batch Stochastic Gradient Descent.” SIGMOD 2019.
The proposed tuple-oriented compression technique is reminiscent of the Lempel-Ziv-Welch (LZW) compression algorithm, but has some important differences. In the first phase the input table is converted into a sparse representation. Each row in the sparse representation has removed any empty columns and stores the column index as the prefix for each non-empty column. The second phase, logical encoding, checks for repeated sequences of (column index, value) pairs in the table and replaces them with a pointer to a dictionary entry. (Since many of these sequences have common prefixes, the dictionary is a prefix tree structure.) The last phase, physical encoding, uses variable-length data encoding and value indexing to further reduce the storage size of the prefix tree and encoded table structures. This compression technique achieves compression ratios between 10× – 50× for datasets with moderate sparsity, which is 2× – 3× better than compressing with Snappy. The performance of matrix operations on compressed data ranges from 2.5× slower to 10,000× faster than compressing with Snappy, depending on the sparsity of the input data and the matrix operation being performed. It is likely that the performance will further improve by better utilizing hardware parallelism, if compression and decompression are offloaded to hardware.
Fast unbiased sampling for machine learning
A common operation in machine learning pipelines is sampling. The need of sampling arises in two different parts of a machine learning pipeline. First, given that model training has a significant computation cost, users often make modeling decisions (such as what model, features and hyperparameters to use) on a small, representative subset of the dataset. A new class of systems, exemplified by BlinkML, are designed to train approximate models with quality guarantees using a sample. The quality guarantee ensures that with high probability the approximate model on a sample of the data will make the same predictions as the model trained on the entire dataset. Second, during the training phase many algorithms are designed to operate in mini-batches. These are random samples of the dataset that are obtained without replacement. This is commonly done by randomly permuting the dataset, which is very expensive. Both use cases point to a need for an efficient unbiased sampling primitive for massive datasets.
About the author: Spyros Blanas is an Assistant Professor in the Department of Computer Science and Engineering at The Ohio State University. His research interest is high performance database systems. Ce Zhang contributed to the development of the ideas in this post.
Disclaimer: These posts are written by individual contributors to share their thoughts on the Computer Architecture Today blog for the benefit of the community. Any views or opinions represented in this blog are personal, belong solely to the blog author and do not represent those of ACM SIGARCH or its parent organization, ACM.


